 W
WCentralne twierdzenie graniczne – jedno z najważniejszych twierdzeń rachunku prawdopodobieństwa, uzasadniające powszechne występowanie w przyrodzie rozkładów zbliżonych do rozkładu normalnego.
 W
WCiągły rozkład prawdopodobieństwa – rozkład prawdopodobieństwa, dla którego dystrybuanta jest funkcją ciągłą. Stosowana jest też węższa definicja, przedstawiona poniżej w sekcji bezwzględna ciągłość.
 W
WDyskretny rozkład prawdopodobieństwa – rozkład prawdopodobieństwa zmiennej losowej dający się opisać przez podanie wszystkich przyjmowanych przez nią wartości, wraz z prawdopodobieństwem przyjęcia każdej z nich. Funkcja przypisująca prawdopodobieństwo do konkretnej wartości zmiennej losowej jest nazywana funkcją rozkładu prawdopodobieństwa. Zachodzi:
 W
WPrawo Zipfa lub prawo Estoupa-Zipfa – prawo opisujące zasadę częstotliwości użycia w dowolnym języku poszczególnych wyrazów. Głosi ono, że jeżeli dla jakiegokolwiek tekstu lub grupy tekstów ustala się wykaz wyrazów ułożonych w malejącym porządku częstotliwości ich występowania, to ranga wyrazu jest odwrotnie proporcjonalna do częstotliwości, zatem iloczyn częstotliwości i rangi powinien być wielkością stałą.
 W
WRozkład arcusa sinusa – rozkład prawdopodobieństwa, którego dystrybuanta wyraża się wzorem
 W
WRozkład Benforda – rozkład prawdopodobieństwa występowania określonej pierwszej cyfry w wielu rzeczywistych danych statystycznych, np. dotyczących powierzchni jezior, danych z rocznika statystycznego, wartościach stałych fizycznych. Ogólnie rozkład ten sprawdza się w przypadku wielkości, które mogą przyjmować różne rzędy wielkości. Fakt częstego występowania tego rozkładu w obserwowanych danych zwany jest prawem Benforda.
 W
WRozkład beta – rodzina ciągłych rozkładów prawdopodobieństwa zadana za pomocą funkcji gęstości
 W
WRozkład Boltzmanna – stosowane w fizyce i chemii równanie określające sposób obsadzania stanów energetycznych przez atomy, cząsteczki lub inne indywidua cząsteczkowe (cząstki) w stanie równowagi termicznej.
 W
WRozkład Pareta – ciągły rozkład prawdopodobieństwa, spełniający potęgowe prawo skalowania, występujący m.in. w naukach społecznych, geofizyce i aktuariacie. Poza ekonomią jest czasem nazywany rozkładem Bradforda.
 W
WRozkład Cauchy’ego to rozkład prawdopodobieństwa typu ciągłego.Momenty zwykłe i centralne rozkładu są niezdefiniowane – odpowiednie całki rozbiegają się do nieskończoności. Oznacza to też m.in., że nie można zdefiniować kurtozy i skośności. Jeśli niezależne zmienne losowe X i Y mają standardowy rozkład normalny, to zmienna X/Y ma rozkład Cauchy’ego z parametrami x0 = 0 i γ = 1
 W
WRozkład chi to rozkład prawdopodobieństwa typu ciągłego.
 W
WRozkład chi kwadrat – rozkład zmiennej losowej, która jest sumą kwadratów niezależnych zmiennych losowych o standardowym rozkładzie normalnym. Liczbę naturalną nazywa się liczbą stopni swobody rozkładu zmiennej losowej.
 W
WRozkład Dirichleta – rodzina ciągłych rozkładów prawdopodobieństwa wielu zmiennych, określona wektorem dodatnich liczb rzeczywistych. Stanowi uogólnienie rozkładu beta w przestrzeni wielu zmiennych. Rozkład Dirichleta jest często używany w rachunku prawdopodobieństwa wraz z twierdzeniem Bayesa jak rozkład aprioryczny i faktycznie rozkład Dirichleta jest rozkładem komunigacyjnym rozkładu dyskretnego. W efekcie funkcja rozkładu zwraca przekonanie, że prawdopodobieństwo możliwych zdarzeń losowych wynosi biorąc pod uwagę, że każde zdarzenie zostało zaobserwowane razy.
 W
WRozkład dwumianowy – dyskretny rozkład prawdopodobieństwa opisujący liczbę sukcesów w ciągu niezależnych prób, z których każda ma stałe prawdopodobieństwo sukcesu równe Pojedynczy eksperyment nosi nazwę próby Bernoulliego.
 W
WRozkład dzeta – dyskretny rozkład prawdopodobieństwa, będący granicą rozkładu Zipfa dla parametru N dążącego do nieskończoności.
 W
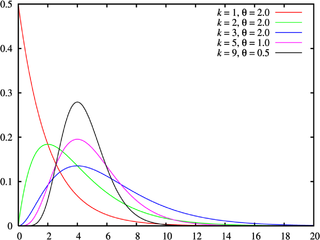
WRozkład Erlanga – ciągły rozkład prawdopodobieństwa, związany z rozkładem wykładniczym i rozkładem gamma. Rozkład Erlanga został opracowany przez A.K. Erlanga do szacowania liczby rozmów telefonicznych, łączonych jednocześnie przez operatora w ręcznej centrali telefonicznej. Później uwzględniono również czas oczekiwania w kolejce. Obecnie rozkład ten znalazł też zastosowanie w teorii procesów stochastycznych.
 W
WRozkład F Snedecora – rozkład prawdopodobieństwa zmiennej losowej F o d1, d2 stopniach swobody.
 W
WRozkład Fishera-Tippetta – rozkład zmiennej losowej służący do wyznaczania ekstremalnych wartości zmiennej losowej w pewnym przedziale czasu. Większość losowych zjawisk naturalnych daje się dobrze opisywać tym rozkładem.
 W
WRozkład gamma – ciągły rozkład prawdopodobieństwa, którego gęstość jest uogólnieniem rozkładu Erlanga na dziedzinę dodatnich liczb rzeczywistych. Rozkład gamma ze względu na klasyfikację Pearsona jest rozkładem typu 3.
 W
WRozkład geometryczny – dyskretny rozkład prawdopodobieństwa opisujący prawdopodobieństwo zdarzenia, że proces Bernoulliego odniesie pierwszy sukces dokładnie w -tej próbie. musi być liczbą naturalną dodatnią. Rozkład ten oznacza się zwykle symbolem Geo(p).
 W
WRozkład jednostajny – ciągły rozkład prawdopodobieństwa, dla którego gęstość prawdopodobieństwa w przedziale od a do b jest stała i różna od zera, a poza nim równa zeru. Istnieje też wersja dyskretna tego rozkładu oraz uogólnienie na dowolne nośniki.
 W
WRozkład jednostajny dyskretny – dyskretny rozkład prawdopodobieństwa w którym jednakowe prawdopodobieństwo przypisane jest do różnych liczb rzeczywistych a inne liczby mają przypisane prawdopodobieństwo zero.
 W
WRozkład logarytmicznie normalny – ciągły rozkład prawdopodobieństwa dodatniej zmiennej losowej, której logarytm ma rozkład normalny.
 W
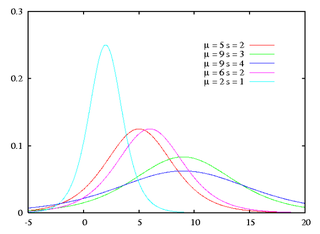
WRozkład logistyczny – ciągły rozkład prawdopodobieństwa używany w szczególności do opisu analitycznego procesów wzrostu osiągających stan wysycenia.
 W
WRozkład Maxwella – wzór określający rozkład prędkości cząstek gazu doskonałego, w którym poruszają się one swobodnie i nie oddziałują ze sobą, z wyjątkiem bardzo krótkich zderzeń sprężystych, w których mogą wymieniać pęd i energię kinetyczną, ale nie zmieniają swoich stanów wewnątrzcząsteczkowych. Cząstka w tym kontekście oznacza zarówno atomy, jak i cząsteczki.
 W
WRozkład normalny, rozkład Gaussa – jeden z najważniejszych rozkładów prawdopodobieństwa, odgrywający ważną rolę w statystyce. Wykres funkcji prawdopodobieństwa tego rozkładu jest krzywą w kształcie dzwonu.
 W
WRozkład Pareta – ciągły rozkład prawdopodobieństwa, spełniający potęgowe prawo skalowania, występujący m.in. w naukach społecznych, geofizyce i aktuariacie. Poza ekonomią jest czasem nazywany rozkładem Bradforda.
 W
WRozkład Pascala – dyskretny rozkład prawdopodobieństwa opisujący m.in. liczbę sukcesów i porażek w niezależnych i posiadających równe prawdopodobieństwo sukcesu próbach Bernoulliego. Jest uogólnieniem rozkładu geometrycznego dla wielu prób.
 W
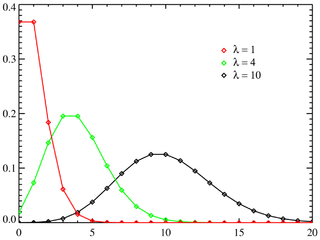
WRozkład Poissona – dyskretny rozkład prawdopodobieństwa, wyrażający prawdopodobieństwo szeregu wydarzeń mających miejsce w określonym czasie, gdy te wydarzenia występują ze znaną średnią częstotliwością i w sposób niezależny od czasu jaki upłynął od ostatniego zajścia takiego zdarzenia. Rozkład Poissona można również stosować w odniesieniu do liczby zdarzeń w innych określonych przedziałach, takich jak odległość, powierzchnia lub objętość.
 W
WRozkład Rayleigha – ciągły rozkład prawdopodobieństwa powstający jako rozkład długości wektora na płaszczyźnie, którego składowe są niezależnymi zmiennymi losowymi o rozkładzie normalnym. Jest rozkładem jednoparametrycznym i stanowi szczególny przypadek rozkładu Weibulla.
 W
WRozkład Skellama jest dyskretnym rozkładem prawdopodobieństwa różnicy dwóch statystycznie niezależnych zmiennych losowych and z których każdy ma rozkład Poissona z różną wartością oczekiwaną and Jest to przydatne w opisie statystyk różnicy dwóch obrazów z prostym szumem śrutowym, a także w opisie rozkładów zakładów finansowych w niektórych sportach jak baseball, hokej i piłka nożna.
 W
WRozkład Studenta – ciągły rozkład prawdopodobieństwa stosowany często w statystyce w procedurach testowania hipotez statystycznych i przy ocenie niepewności pomiaru. Przy opracowaniu wyników pomiarów często powstaje zagadnienie oszacowania przedziału, w którym leży, z określonym prawdopodobieństwem, rzeczywista wartość mierzona, jeśli dysponujemy tylko wynikami n pomiarów, dla których możemy wyznaczyć takie parametry, jak średnia i odchylenie standardowe lub wariancja , nie znamy natomiast odchylenia standardowego w populacji. Zagadnienie to rozwiązał w 1908 r. William Sealy Gosset podając funkcję zależną od wyników pomiarów a niezależną od
 W
WRozkład trójkątny to ciągły rozkład prawdopodobieństwa zmiennej losowej.
 W
WRozkład wykładniczy – rozkład zmiennej losowej opisujący sytuację, w której obiekt może przyjmować stany i przy czym obiekt w stanie może ze stałym prawdopodobieństwem przejść w stan w jednostce czasu. Prawdopodobieństwo wyznaczane przez ten rozkład to prawdopodobieństwo przejścia ze stanu w stan w czasie
 W
WStatystyka Fermiego-Diraca – statystyka dotycząca fermionów, cząstek o spinie połówkowym, które obowiązuje zakaz Pauliego. Zgodnie z zakazem Pauliego w danym stanie kwantowym nie może znajdować się więcej niż jeden fermion. Statystyka Fermiego-Diraca oparta jest również na założeniu nierozróżnialności cząstek.
 W
WWielowymiarowy rozkład normalny – rozkład wielowymiarowej zmiennej losowej, będący uogólnieniem rozkładu normalnego na n wymiarów.
 W
WWzór Breita-Wignera, rozkład Breita-Wignera – wzór ciągłego rozkładu zmiennej losowej wyrażany wzorem: